Filter Bank Common Spatial Patterns and Filterbank Network#
Filter Bank Common Spatial Patterns (FBCSP) is a strong feature-based baseline
Learns spatial topography of task-related spectral power changes
Widely used for (movement-related) EEG-decoding
We used it as a starting point for our network architecture development
In a prior master thesis [Schirrmeister, 2015], we had developed a neural network architecture closely resembling the feature-based decoding algorithm filter bank common spatial patterns. In this chapter, I describe filter bank common spatial patterns as well as the corresponding filter bank network of the prior master thesis as the starting point for the network architectures developed in the context of this thesis.
\(\require{color}\) \(\definecolor{commentcolor}{RGB} {70,130,180}\)
Filter Bank Common Spatial Patterns as a Starting Point#
We selected filter bank common spatial patterns (FBSCP [Ang et al., 2008, Chin et al., 2009]) as the feature-based EEG-decoding algorithm we were trying to imitate in our initial neural network architectures. FBCSP is an EEG-decoding algorithm that has been successfully used in task-related EEG-decoding competitions [Tangermann et al., 2012]. FBCSP aims to decode task-related changes in signal amplitude in different frequencies, such as a decrease in the amplitude of alpha and beta-band oscillations during movement imagination. In the following, we will explain how FBCSP decodes two classes of EEG signals by finding frequency-specific spatial filters that transform the signal, such that it has relatively high variance for one class and low variance for the other class and vice versa.
Common Spatial Patterns#
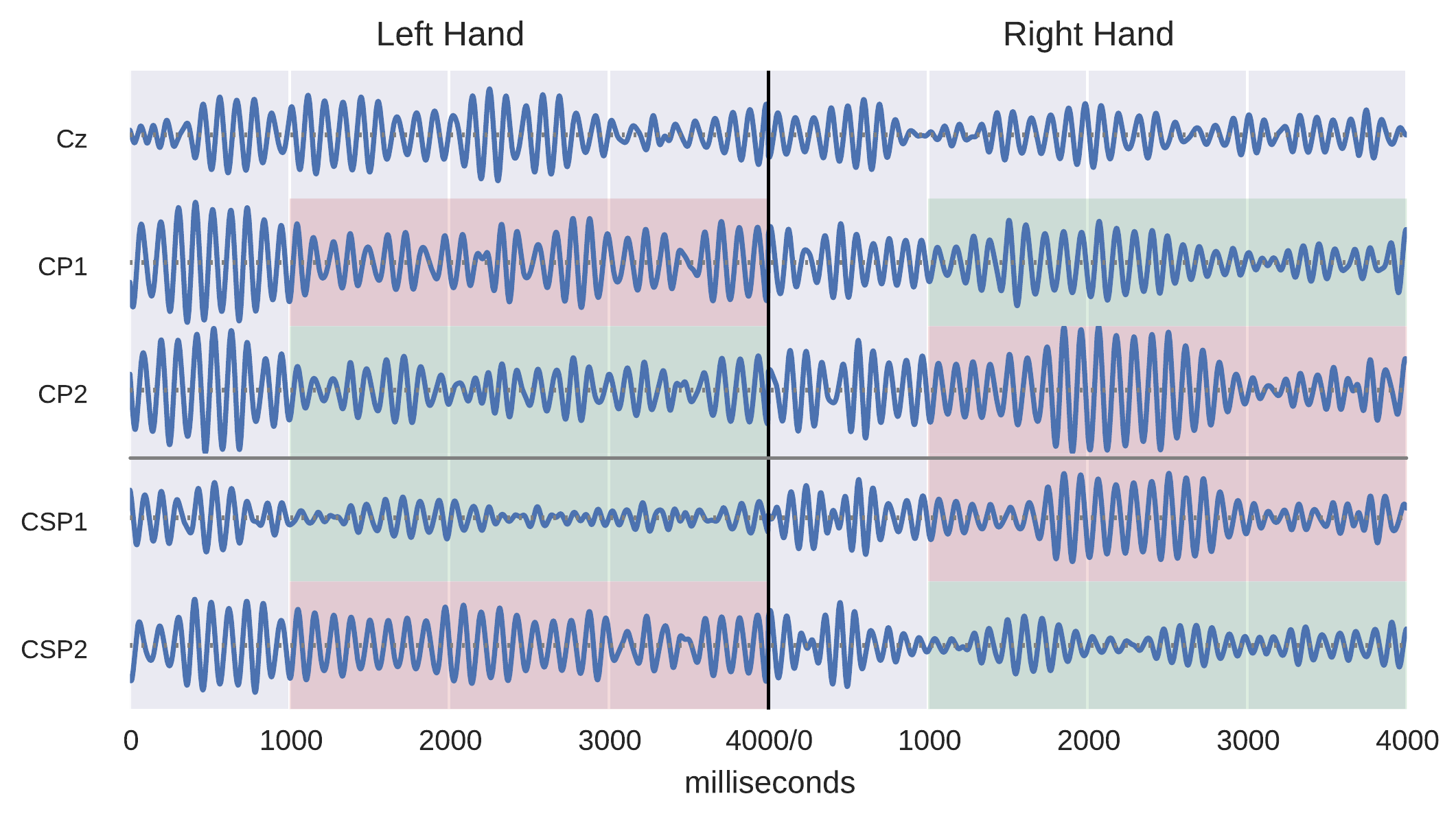
Fig. 3 Common Spatial Patterns example taken from a master thesis [Schirrmeister, 2015]. Top parts show EEG signals for three electrodes during a left hand and a right hand movement. Bottom parts show spatially filtered signals of two CSP filters. Green parts have lower variance and red parts have higher variance. Note that this difference is strongly amplified after CSP filtering.#
The basic building block of FBCSP is the common spatial patterns (CSP) algorithm. CSP is used to decode neuronal activity that leads to a change in the amplitudes of the EEG signal with a specific spatial topography [Blankertz et al., 2008, Koles et al., 1990, Ramoser et al., 2000]. To do that, CSP aims to maximize the ratio of the signal variance between spatially filtered signals of two classes, e.g. of the signal during two different movements. For example, the signal of a spatial filter computed by CSP may have a very large variance during movements of the left hand and a very small variance during movements of the right hand. Concretely, we are given signals \(X_{1}, X_{2} \in \mathbb{R}^{n x k x t}\) from \(n\) EEG trials (can be different for \(X_1, X_2\)), \(k\) EEG electrodes and \(t\) timepoints within each trial. CSP then finds a spatial filter \(w\) that maximize the ratio of the variances of the spatially filtered \(X_1,X_2\):
\(w=\arg\!\max_w\frac{Var(w^T X_1)}{Var(w^T X_2)}= \arg\!\max_w\frac{||w^T X_1||^2}{||w^T X_2||^2}=\arg\!\max_w\frac{w^T X_1 X_1^T w}{w^T X_2 X_2^T w}\)
Rather than just finding a single spatial filter \(w\), CSP is typically used to find a whole matrix of spatial filters \(W^{kxk}\), with spatial filters ordered by the above variance ratio and orthogonal to each other. The first filter \(w_1\) results in the largest variance ratio and the last filter \(w_k\) results in the smallest variance ratio. Different algorithms can then be used to subselect some set of filters to filter signals for a subsequent decoding algorithm.
The CSP-filtered signals can be used to construct features to train a classifier. Since the CSP-filtered signals should have very different variances for the different classes, the natural choice is to use the per-trial variances of the CSP-filtered signals as features. This results in as many features per trial as the number of CSP filters that were selected for decoding. Typically, one applies the logarithm to the variances to get more standard-normally distributed features.
Filter Bank Common Spatial Patterns#
CSP is typically applied to an EEG signal that has been bandpass filtered to a specific frequency range. The filtering to a frequency range is useful as brain signals cause EEG signal amplitude changes that are temporally and spatially different for different frequencies [Ang et al., 2008]. For example, during movement the alpha rhythm may be suppressed for multiple electrodes covering a fairly large region on the scalp while the high gamma rhythm would be amplified for a few electrodes covering a smaller region.
Filter bank common spatial patterns applies CSP separately on signals bandpass-filtered to different frequency ranges [Ang et al., 2008, Chin et al., 2009]. This allows to capture multiple frequency-specific changes in the EEG signal and can also make the decoding more robust to subject-specific signal characteristics, i.e., which frequency range is most informative for a given subject. The trial-log-variance features of each frequencyband and each CSP filter are then concatenated to form the entire trial feature vector. Typically, a feature selection procedure will select a subset of these features to train the final classifier.
The overall FBCSP pipeline hence looks like this:
Bandpass filtering: Different bandpass filters are applied to separate the raw EEG signal into different frequency bands.
Epoching: The continuous EEG signal is cut into labeled trials, e.g., 4-second left-hand or right-hand movement windows.
CSP computation: Per frequency band, the common spatial patterns (CSP) algorithm is applied to extract spatial filters (see Common Spatial Patterns).
Spatial filtering: The spatial filters computed in Step 2 are applied to the EEG signal.
Feature construction: Feature vectors are constructed from the filtered signals: Specifically, feature vectors are the log-variance of the spatially filtered trial signal for each frequency band and for each spatial filter.
Feature selection: A feature selection algorithm may be used to only retain a subset of the features for classification.
Classification: A classifier is trained to predict per-trial labels based on the feature vectors.
Filter Bank Network Architecture#
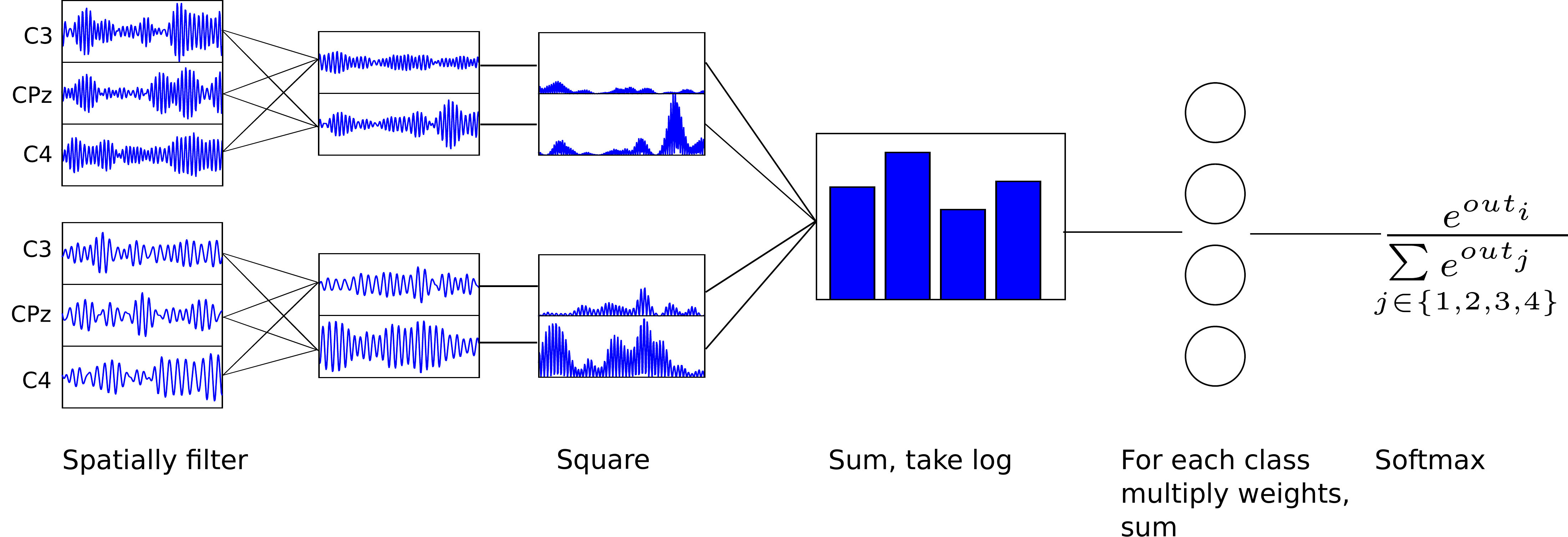
Fig. 4 Filter bank network architecture overview. Input signals were bandpass filtered to different frequency ranges. Signals are first transformed by learned spatial filters, then squared, summed and the log-transformed. The resulting features are transformed into class probabilities by a classification weights followed by the softmax function. Taken from a master thesis [Schirrmeister, 2015].#
The first neural network architecture was developed by us in a prior master thesis [Schirrmeister, 2015] to jointly learn the same steps that are learned separately by FBCSP (see Fig. 4). Concretely, the network simultaneously learn the spatial filters across many frequency bands and the classification weights for the log squared sums of all resulting spatially filtered signals. To be able to do that, the network is fed with input EEG signals that were bandpass-filtered to different frequency ranges. The network then performs the following steps:
Spatial Filtering
\( \begin{align*} h_1 &= W_s^Tx && \color{commentcolor}{\text{Apply learnable spatial filter weights } W_s \text{ to inputs }} \\ \end{align*} \)
Feature Construction
\( \begin{align*} h_2 &= h_1^2 && \color{commentcolor}{\text{Square the spatially filtered signals }} \\ h_3 &=\sum_t (h_2) && \color{commentcolor}{\text{Sum the squared signals across all timepoints t with a trial }} \\ h_4 &= \log(h_3) && \color{commentcolor}{\text{Take the logarithm of the summed values}}\\ \end{align*} \)
Classification
\( \begin{align*} h_5 &= W_c^Th_4 && \color{commentcolor}{\text{Apply learnable classifier weights } W_c \text{ on these "log-variance" features }} \\ p(c_i|h_5) &= \frac{e^{h_{5,i}}}{\sum_j e^h_{5,j}} && \color{commentcolor}{\text{Take the softmax to produce per-class predictions }} \\ \end{align*} \)
The spatial filter weights and the classification weights are trained jointly.
Open Questions
How does the filterbank net compare to FBCSP?
What can more generic architectures look like?